Deux types de complexité
(il n’en restera qu’un)
Pour commencer, distinguons tout de suite deux types de complexité : l’une temporelle, l’autre spatiale. La complexité temporelle permet d’ évaluer quel va être la rapidité d’exécution d’un algorithme en fonction d’un ou de plusieurs paramètres dépendant de la ou des données fournies en entrée. La complexité spatiale, quant à elle, permet d’évaluer l’occupation mémoire que va nécessiter un algorithme en fonction (toujours) de certains paramètres.
Si l’intérêt de la complexité temporelle semble évident pour étudier la vitesse, les performances, ou la capacité à supporter la charge, je ne vous apprendrai rien en vous disant que de nos jours la mémoire n’est plus un paramètre réellement limitant. D’une part le prix de la RAM a beaucoup baissé durant les vingt dernières années et d’autre part, la mémoire virtuelle est également une réponse à ce problème. Nous allons donc délaisser la complexité spaciale des algorithmes pour nous pencher que leur complexité temporelle.
Unité de mesure et paramètre d’expression
(je ne suis pas un numéro !)
Evaluer le temps pris par un algorithme, fort bien, mais sur la base de quelle unité ? Imaginons que nous choisissions la seconde. Ce n’est pas un bon choix ! En effet, la vitesse des microprocesseurs ne cesse d’évoluer, donc une mesure de temps faite aujourd’hui n’aurait plus aucun sens dans quelques années à peine !
Choisissons donc une unité plus représentative de la charge de calcul, comme par exemple le nombre de fois que l’on va exécuter l’instruction la plus coûteuse. C’est justement le choix le plus habituel. Pour illustrer ce choix voyez plutôt les deux exemples suivants.
- Pour un algorithme de tri, l’instruction la plus coûteuse est la comparaison de deux objets.
- Pour une multiplication de polynomes ou de matrices, ce sont les opérations arithmétiques « + » et « * ».
Ensuite, le paramètre qui va nous permettre d’exprimer ce nombre d’exécutions sera par exemple la longueur n d’une liste, la hauteur n d’un arbre ou l’indice n lorsque qu’il s’agit de calculer le n-ème terme d’une suite. Il est aussi possible d’utiliser plusieurs paramètres. Par exemple, pour une fonction faisant l’union de deux arbres a et b, la complexité pourra dépendre de leurs hauteurs respectives que l’on notera par exemple |a| et |b|.
Deux outils mathématiques
(le marteau et la tenaille)
Nous savons quelle unité choisir, donc nous allons pouvoir exprimer nos complexité. Super ! Mais si nous avons le choix entre deux algorithme ayant deux complexités différentes, comment savoir lequel est le meilleur ? C’est là que l’outil mathématique intervient. Il va nous permettre de comparer les complexités.
La notaton « grand O de »
Soit f et g deux applications à variable entière. On dit que f est un grand O de g [à l’infini : ceci est sous-entendu lors de la comparaison de deux fonctions à variables entières (ie des suites)] (et on écrit f=O(g)) s’il existe un réel A tel que |f(n)|<A*|g(n)| pour tout n entier positif.
La propriété suivante est bien pratique :
na=O(nb) si et seulement si a<=b
On a aussi le résultat (qui permet de simplifier des calculs) :
si f=O(g) et g>=0 alors S(f(k),k=1..n)=O(S(g(k),k=1..n)) où S(u(k),k=1..n)=u(1)+...+u(n)
si f=O(g) on dit aussi que f est dominée par g. Cette relation de domination est réflexive et transitive. C’est-à-dire :
* f=O(f) quel que soit f * si f=O(g) et g=O(h) alors f=O(h)
mais n’est pas symétrique :
soit a<b, alors na est dominée par nb mais nb n’est pas dominée par na
La notation « grand thêta » [1]
Si f et g sont deux applications à variables entières, on dit que f et g sont du même ordre de grandeur si f=O(g) et g=O(f) : on note f=thêta(g).
Ainsi, avec un grand O, on sait à quoi s’attendre dans le pire des cas alors qu’avec un grand thêta, on sait à quoi s’attendre tout le temps. En général, on utilise surtout le grand O.
Classification des complexités
(le podium et les médailles)
Grâce à notre nouvel outil « O » nous allons pouvoir comparer les complexités entre elles. Mais pour commencer, illustrons les complexités les plus classiques par la représentation suivante :
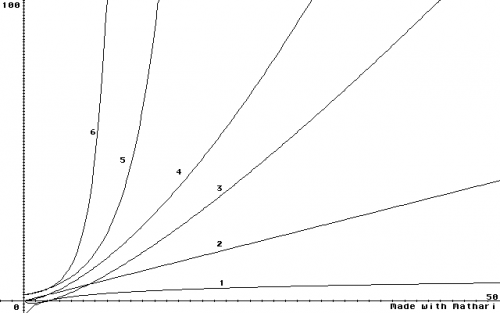
- complexité logarithmique en O(ln(n)) (ou lnk(n), k>1)
- complexité linéaire en O(n)
- complexité quasi-linéaire en O(n*ln(n))
- complexité polynômiale en O(nk) (k>1)
- complexité exponentielle en O(an) (a>1)
- complexité hyperexponentielle comme O(n!) ou pire, O(nn) : aïe ! Révisez votre algorithme !
Notez que les complexité « lourdes » du type exponentielle ou pire sont parfois inévitables pour résoudre certains problèmes particuliers. Ainsi, les problèmes qui appartiennent à une catégorie que l’on nomme NP-complets ne peuvent se satisfaire au mieux que d’algorithmes à complexité exponentielle. Dans ce genre de situation, peu importe la machine, peu importe le langage, peu importent les optimisations géniales du programmeur, il suffit d’augmenter légèrement n pour écrouler n’importe quelle machine sous la charge de calcul ! De quoi déprimer n’importe que codeur en assembleur mais on n’y peut rien, c’est la vie !
A l’inverse, le top du top, c’est la complexité logarithmique. Quand vous avez un algorithme de ce genre, c’est merveilleux. Vous avez beau augmenter n dans des proportions ahurissantes, votre machine tiendra la charge !
Exprimer une complexité
(ne soyez pas timides)
Pour vous donner une idée de la façon dont vous pouvez évaluer la complexité de vos algorithmes, rien de mieux que quelques exemples. Voici donc quelques calculs simples de complexité :
Calcul récursif de factorielle
Soit la fonction récursive suivante en GFA-Basic :
nous allons mesurer la complexité de cette fonction en comptant le nombre d’exécutions de « l’instruction * », c’est-à-dire l’opération de multiplication.
Soit n l’entier dont on veut calculer la factorielle et T(n) le nombre d’opérations « * » que nécessite le calcul de n!.
On a : T(0)=T(1)=0 pour calculer n!, on calcule (n-1)! et on multiplie par n, d’où T(n)=1+T(n-1) finalement, on peut expliciter T(n) pour tout n : on a évidemment T(n)=n-1 pour n>0, T(0)=0 or n-1=O(n) donc T(n)=O(n), la complexité de cet algorithme est donc en O(n) : complexité linéaire.
Tri par sélection d’un tableau
plus haut dans le texte, nous avons vu que pour un tri, on choisissait comme opération la plus coûteuse la comparaison, on peut choisir aussi le nombre d’échanges. Nous allons donc successivement déterminer la complexité du tri par sélection en comparaisons et en échanges. Soit T(n) la complexité en comparaison et U(n) la complexité en échanges.
- calcul de T(n)
1 comparaison est effectuée à chaque exécution de la boucle FOR-NEXT interne donc
T(n)=(n-1)+(n-2)+...+1=n*(n-1)/2 (calcul classique)
et n(n-1)/2=O(n2)
donc T(n)=O(n2) - calcul de U(n)
1 échange est effectuée à chaque exécution de la boucle FOR-NEXT externe donc
U(n)=1+...+1 (n-1 fois) donc U(n)=n-1
et n-1=O(n)
donc U(n)=O(n)
Le tri par sélection est donc un très bon tri si l’opération la plus coûteuse à exécuter est l’affectation de données (et donc l’échange de deux éléments du tableau) mais est un assez mauvais tri si c’est la comparaison des données qui est la plus coûteuse. En fait, les bons tris en ce qui concerne le nombre de comparaisons sont le tri par fusion, le célèbre Quick Sort, etc. Leur complexité en comparaisons est en O(n*ln(n)) pour le tri fusion et O(n*ln(n)) pour le quick-sort dans le cas moyen. Ainsi, il arrive que l’on calcule la complexité d’un algorithme dans le cas moyen et dans le pire des cas : pour le Quick Sort, le pire des cas est celui où les données sont déjà triées ! A noter qu’il existe un théorème qui dit que pour un algorithme général [2] de tri des données, on ne peut pas faire mieux que O(n*ln(n)) pour la complexité en comparaisons dans le cas moyen.
Conclusion
(faites « au revoir » de la main)
Voilà pour cette courte intrusion dans la théorie. La prochaine fois, je parlerais exclusivement de programmation mais je ne sais pas encore à quel sujet. D’ici là, portez-vous bien et essayez d’évaluer la complexité de vos algorithmes ; vous vous rendrez parfois compte qu’un petit changement de point de vue (donc d’algorithme) est bougrement nécessaire !